ジグのフォール速度と姿勢を手計算で求めてみた

1秒間でジグがフォールする距離は、
ダイソーの『ジグロック』18gは1.66m。
『ジグロック』40gは1.93m。
同じくダイソーの『メタルジグ』18gは2.13m。
ダイソージギンガーの皆様、この数字は肌感覚と合っているでしょうか。
当サイトは、100均のジグを使ったショアジギングをテーマにしていますが、今回は手計算で求めたジグの速度とフォール姿勢についての考察を書いてみたいと思います。
計算してみようと思った動機
以前から、100均ジグがフォールするときは縦の姿勢(ラインアイが上)になっていると考えていましたが、2022年の企画「100均ジグの弱点をカバーしてくれるようなジグを探そう」ということで、各種メーカーサイトやユーザーのインプレ記事を調べてみたところ、ジグのフォール姿勢や速度については、様々な考え方があることを改めて感じました。
いろいろと調べたことをざっくりまとめてみると、
フォール速度については、細身形状のジグの方が平たくて表面積が大きいジグよりも速いという意見でほぼ統一されています。
スローに誘う釣り方を特に「ショアスロー」と命名してジャンルをつくり、ショアスロー用の幅が広い(表面積の大きい)ジグを各メーカーが売り出していますので、表面積と速度の関係はほぼ統一見解となっているようです。
個人的な経験からも、ダイソーのメタルジグ(表面積が小さく、細身)の方がジグロック(太身で表面積が大きい)よりもフォール速度が速いと感じているので、異論はありません。
次に、フォール姿勢については、ヒラヒラ、水平、バイブレーション、すとんと落ちる、滑走する、この形状が〇〇なアクションを生む…等いろいろありました。
個人的には、ダイソージグのフォール姿勢は、ヒラヒラや水平姿勢はかなり限られた条件でした起こらないと考えています。
100均のジグとメーカーのジグはフォール速度やフォール姿勢がどう違うのか、常に水平姿勢になるのか、それとも限られた状況でしか起こらないのか、そもそも自分の感覚は間違っているのではないか。
こうした疑問を計算によって少しでもクリアにできないかと考えたのでした。
計算対象のジグは3つ
今回、計算対象としたのは、以下の100均ジグです。
・ジグロック18g ←ダイソージグの太い方です(下の画像参照)。セリアでは同じ形状で色違いのものが『メタルジグ』というネーミングで売られています。個人的に最も良く使用するジグです。
・ジグロック40g ←ジグロック18gと比較するために40gでも計算してみました。
・メタルジグ18g ←ダイソージグの細い方です。ジグロック18gと同じ重さなので、違いは形状です。

シミュレーションは4パターン
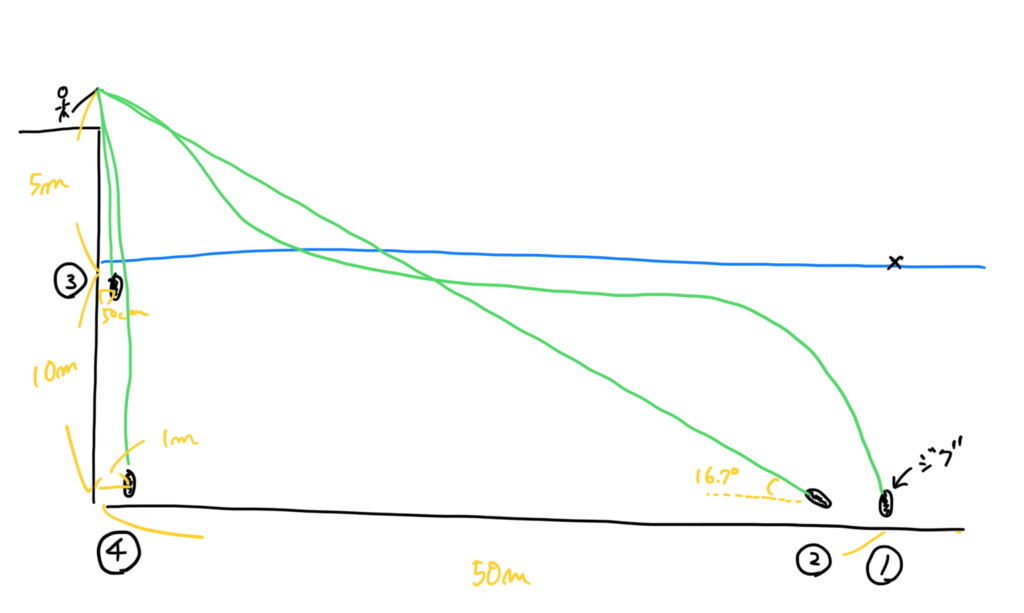
① キャスト後、フリーフォールさせ、ボトム着底直前のジグ
② ①でボトム着底し、糸フケ回収後に1mリフトした後にフォールさせたときのジグ
③ 足元水深1mでフリーフォールさせたときのジグ
④ 足元水深10mでフリーフォールさせたときのジグ
この4パターンのジグのフォール速度と姿勢について考えていきます。
注意事項
・この記事には数字や数式が出てきます。数学・物理アレルギーの方は少し覚悟してください。
・モデル計算には前提条件があります。大まかな前提条件は次の項で説明しますが、前提条件が整わない場合は計算結果が崩れます。
・使用する公式と計算はシンプルなものを採用しました。他者のチェックを受けていませんので、はなから見当違いをしていたり、計算ミスは充分ありえます(物理学のセンスはありません)。
・計算ミスがある場合でも、フォールに関係する要素や考え方が釣りのヒントになると思いますので、読みものとしてお楽しみください。
前提条件
シミュレーションの主な前提条件は以下のとおりです。
ここは物理の考え方や公式を知っている人や計算式を見た後で戻る項目なので、現段階は読み飛ばして構いません。
・シミュレーションパターン①②では、竿先から水面まで5m、水深10m、キャスト飛距離50m。
・シミュレーションパターン③④では、竿先から水面まで5m、水深10m。真下にジグを落とそうとしたが、③ではジグは水深1mの位置にあり、真下から50cmブレた(少し前方へ放ったときのイメージ)。④では水深10mの位置にあり、1mブレた(同)。
・使用しているラインの直径は0.2mm(PE1.5号相当)で、ジグに直結。
・ジグについているのはラインのみで、フックやブレードなどは付いていない。
・ジグの速度は一定の状態(手に持っていたボールを勢いをつけず落とすと重力の影響でどんどん速度が上がっていくが、一定の速度までいくとそれ以上速度は上がらなくなる状態=加速度0)。
・ジグロックは直方体、メタルジグは円柱に近似して考える。
・抗力の計算では、D(N)=抵抗係数Cd×密度ρ(kg/m3)×速度U2(m2/s2)×投影面積S(m2)/2 の公式を使う。※文字の後の数字は階乗(m2ならm×m)を表します。
・ジグロックの抗力係数は、垂直(①、③、④)のとき1.2、ナナメのとき(②)は1.35とする。
・メタルジグの抗力係数は、垂直(①、③、④)のとき0.9、ナナメのとき(②)は0.95とする。
・ラインの抗力係数は、1.15とする。
・ジグロックとメタルジグの材質と配合割合は同一で、鉛の密度を11,360(g/m3)とする。
・海水の密度を1,025(g/m3)とする。
・力の釣り合いの式として、【ジグの重量=浮力+鉛直下方向からのジグへの抗力+ラインによる抗力】が成り立つとし、ジグ及びラインへの風や潮流などの他の影響はないものとする。
・シミュレーション①③④でのフォール時のジグの姿勢は、鉛直下向きの状態とする。←後の項で理由を記載します。
シミュレーション①
では、ここから具体的に計算していきます。
シミュレーション①は、竿先から水面まで5mあり、50mキャストして、水深10mの場所。
着水後はフリーフォールさせて、ボトム到着直前のジグの状態です。
有効数字(数字の桁の処理)の表記は、この記事の中では統一しませんのでご了承ください。
ジグロック18gのケース
鉛直下向きにかかるジグの重量Wと、鉛直上向きにかかるジグの浮力F+鉛直上向きにかかるジグへの抗力D+鉛直上向きにかかるラインによる抗力Tが釣り合って、ジグの速度が一定(加速度0)という条件にしましたので、
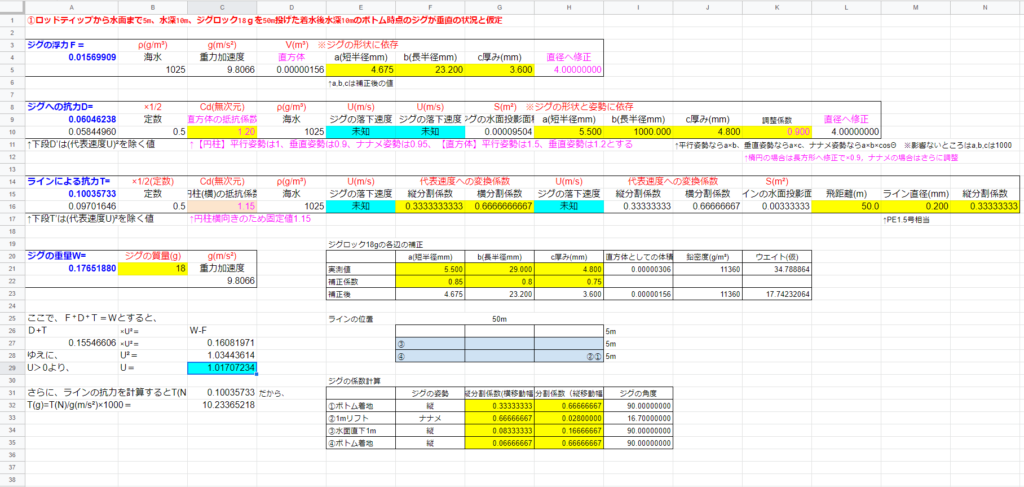
・ジグの重量W(m・kg/s2)=質量m(g)×重力加速度g(m/s2)=18/1000×9.8066≒0.1765
・浮力F(N)=海水密度ρ(g/m3)×重力加速度g(m/s2)×直方体の体積V(m3)=1025×9.8066×0.00000156≒0.015699
※体積は、ジグロックを直方体に見立てて、ジグの各辺の実測最大値×鉛の密度×補正率=ジグの質量から算出。ここでは、短辺半径5.5mm×2/1000×短辺補正率0.85×長辺半径29mm×2/1000×長辺補正率0.8×厚さ4.8㎜/1000×厚さ補正率0.75×鉛密度11,360×単位調整1000≒17.74g≒18gから算出。
・鉛直下方向からのジグへの抗力D(N)=抗力係数Cd×海水密度ρ(kg/m3)×速度U2(m2/s2)×投影面積S(m2)/2=直方体の抗力係数1.2×1025×U2×0.00009504/2≒0.0584496U2
※速度Uはここでは未知数のまま。投影面積は、ボトムから水面に向かってラインに光を当てたときに水面にできる影の面積として計算したもので、ジグを正面(ラインアイの方ついているから見る)から見るといびつな長方形になっているため、短辺実測最大値×厚さ実測最大値×調整係数0.9で長方形に補正して算出。
・ラインのよる抗力T=抗力係数Cd×海水密度ρ(kg/m3)×速度U2(m2/s2)×投影面積S(m2)/2=円柱の抗力係数1.15×1025×U2×α/2≒0.09701646U2
※ラインによる抗力は、ラインが水中を進んだときにかかった力と考える。PEラインは水よりも比重が小さく、また、フリーフォールのため、ロッドティップからジグまでラインは一直線になっていない。そのため、実際にラインにかかった力の投影面積は、ラインの直径×飛距離に調整係数を乗じたものと考える。ここでは、50mのうち2/3、深さ10mのうち1/3しか実際にはラインは動いていないと考えて調整係数を設定した。速度も同様に考えて設定。
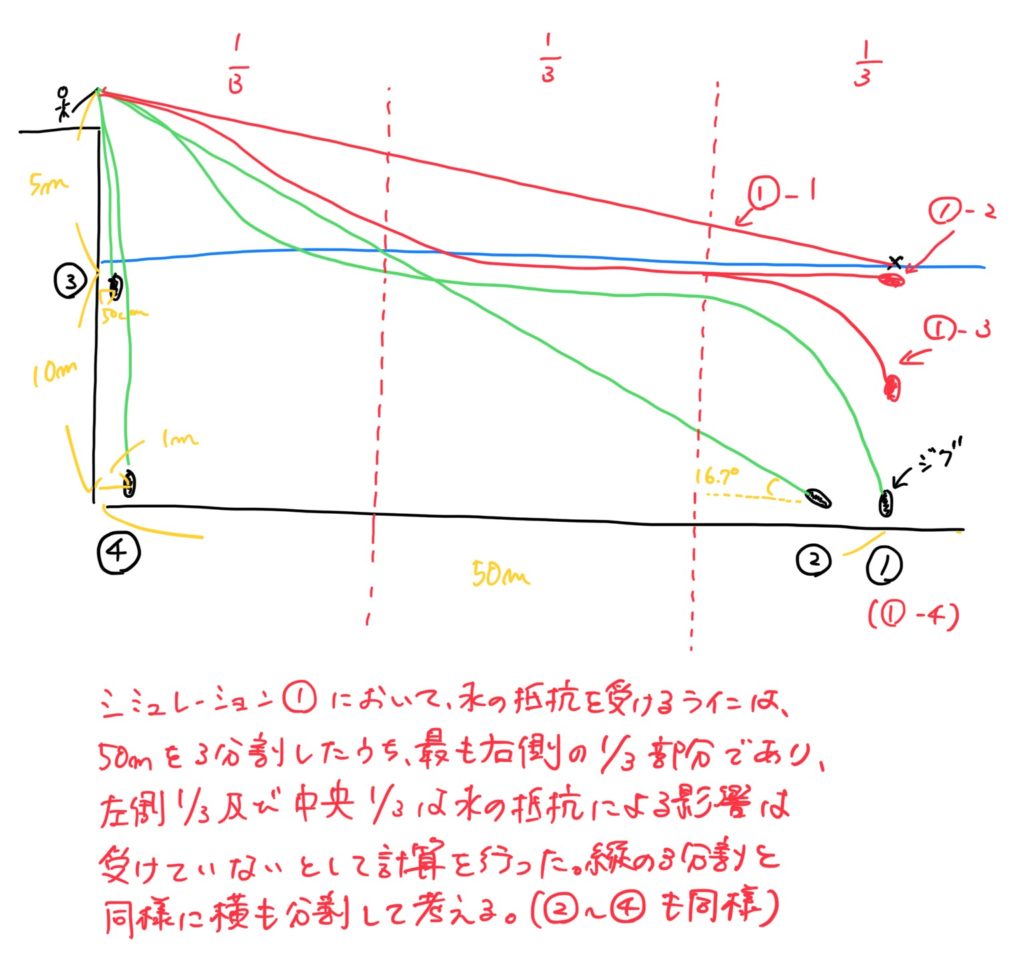
4つの力をそれぞれ計算できたので、W=F+D+Tより、ジグの速度U=1.017(m/s)と計算できました。
ジグロックを直方体と考えたところ、ジグの速度とラインの速度を別としてラインの抗力を計算したところを工夫したのですが、この苦労と感動は伝わりませんね(´;ω;`)。
ジグロック40gのケース
続いてジグロック40gの速度を求めますが、計算過程は省略します。
ジグロック18gと異なるのは、大きさとウエイトです。
それぞれ先ほどと同様に計算すると、ジグの速度U=1.3615(m/s)と計算できました。
メタルジグ18gのケース
こちらも、計算過程は省略します。
ジグロック18gと異なるのは、次のところです。
・物体を円柱に見立てたこと(ジグロックは直方体)
・抗力Dの計算で投影面積の計算する際に、ラインアイ方向から正面に見るとほぼ楕円になっていることからジグロックのように調整係数0.9は用いないこと
計算結果は、ジグの速度U=1.10198(m/s)
シミュレーション①のまとめ
状況と結果を整理します。
ロッドティップから海面まで5m、50mキャストし、水深10mまでフリーフォールで沈めたとき、ボトム直前の1秒間で進む距離は次のとおり。
ジグロック18gは1.017m、ジグロック40gは1.362m、メタルジグ18gは1.102m。
この結果を考察してみます。
ジグロック18gとメタルジグ18gを比較すると、同じ重さならジグロックよりメタルジグの方がフォール速度は速い結果になっています。
これはおそらくメタルジグの形状が細身のためです。
次に、ジグロック18gとジグロック40gを比較すると、多少大きくても重い方がフォール速度は速いという結果になりました。
これはジグロックの形状なら、表面積の増加による抵抗より質量の増加の方が速度に与える影響力は大きいと考えられます。
この結果を見て、肌で感じていたことが数字で証明された感じがしませんか。
ジグの姿勢について
ここで、ジグの姿勢について考えてみましょう。
ダイソーのジグロックとメタルジグは、どちらもセンターバランスです。
つまり、重心がジグの真ん中にあるということでしょう。
それならば、ジグが水平状態になって、ヒラヒラとフォールすることもあり得るんじゃないでしょうか。
実は、さきほどまでごちゃごちゃと計算した中にフォール姿勢を探るヒントがあります。
ポイントになるのはラインによる抵抗です。
これまでの考え方を理解できた方は気づいたかもしれませんが、フォール中はラインがジグに引っ張られていきます。
するとラインは海水を切っていくことになります。
ラインは細いので抵抗は無視できそうですが…一応計算してみましょう。
先ほどの式の中に、ラインによる抵抗の計算式があります。
ラインによる抗力はTというもので、ジグの速度がわかって初めて計算できるものでした。
ジグの速度は計算で導き出したので、改めてラインによる抗力をそれぞれ計算してみると、
ジグロック18gは、0.100(N)≒10.2g
ジグロック40gは、0.392(N)≒18.3g
メタルジグ18gは、0.177(N)≒12.0g
となります。
これまでの計算では、ラインによる抗力Tが働く向きはジグの重量Wと正反対の方向で、作用線は一致している(力が一直線上にあること)ことを前提として計算していました。
TとW作用線が一致しない場合として、ジグが水平姿勢(ジグの最も長い辺がボトムと平行)のときを考えてみます。
ジグはセンターバランスなので、ジグにかかるWはジグのど真ん中から鉛直下向きと考えて差し支えないはずです。
これに対し、ラインがジグを引っ張る力Tは、ラインがジグの片端についていることから、水平姿勢の場合はラインアイから鉛直上向きの力でジグを引っ張っていることになります。
イメージしてみてください。
中心に重心があるジグが水平状態にあり、その端に結んだ糸を10gから18gくらいの力で引っ張ります。
どうでしょう。
ジグの重心を中心として、「回る」ことをイメージできたでしょうか。
重心1点でバランスをとっているとき(水平姿勢)に、どこかに力を加えたらバランスが崩れます。
バランスをとったやじろべえの端に上向きに力をかけると、回る力が働くのと同じイメージです。
これをより一般化した表現にすると、センターバランスのジグは、水の抵抗を受けたラインがジグを引っ張ることにより、水平姿勢の状態であっても、ラインアイを上にした縦向き姿勢(気を付け!状態)になる。
でも、10gくらいなら潮の流れとか、取り付けたフックの抗力とか、その他の条件が重なれば、水平姿勢を保てると思いませんか。
このことについて考えてみると、
水の抵抗を受けたラインがジグを引っ張るとき、ジグが水平姿勢であれば、ラインが引っ張る方向(鉛直上向き)とジグの最長辺とでつくる角度(水平)は90°となり、ジグを回転させようとする力は最も大きくなります。
つまり、何らかのラッキーで水平姿勢になったとしても、ラインにかかる水の抵抗力は、その他の姿勢のときよりも大きな力でかかるので、ジグが回転してラインアイが上向きの姿勢に戻ってしまうということです。
これは、厳密な場合を除いて、センターバランスの形状であればジグのウエイトに関係なく成り立つのでジグロックでもメタルジグでも同じです。
ちなみに、カーブフォールを考えてみると、ラインが水を切る量はフリーフォールよりも多くなりますので、その分水の抵抗は大きくなり、ジグへの抗力Tは増加しますので、水平姿勢の可能性はより低くなると考えられます。
また、フロントフックしかつけないような状況であれば、フックの抗力もジグの片端に加わりますので、より水平フォールの可能性は低くなると考えられます。

フロントフックのみ×ティンセル付フックを使用しているなら、水平姿勢でのフォールの実現性は限りなく低いということになります。
シミュレーション②
次に、シミュレーション②を見てみましょう。
ここまで読んでくれたほとんどの人は、ぐったりしていると思いますので、ここからはさらっといきます。
考え方はシミュレーション①と同じです。
シミュレーション②では、①でボトムをとったあと、1mリフト(1m素早く動いたということが大事で、ジャークでもリーリングでも何でも良い)で引っ張った状態を想定しています。
釣り人の目線で考えると、まっすぐ50m先、そこから15m下にジグがある状態です。
このとき、三角関数を使うとボトムとジグが作る角度は16.7°です。
そこから糸フケを回収してジグまでラインを一直線に張ってからリフトするので、ラインが一直線のままナナメに1m進んだという状況です。
イメージできたでしょうか。
シミュレーション①と大きく異なるのはジグの姿勢です。
ラインを引っ張っていますので、ジグは水平姿勢から16.7°上に向いている状態です(①では90°上向き)。
このことから、フォール時のジグには、水の抵抗が①のときより大きくかかります。
また、ラインは一旦一直線になりますので、その後のフォールにおいて、水を切る量は①と比較するとかなり小さくなりますので、独自の変数を導入して調整しました。
それぞれ速度の計算結果をみると、
ジグロック18gは0.649m、ジグロック40gは0.738m、メタルジグ18gは0.914m。
先ほどと同様に、結果を考察してみます。
ジグロック18gとメタルジグ18gを比較すると、同じ重さならジグロックよりメタルジグの方が速いですね。
これは先ほどと同じく、おそらくメタルジグの形状が細身のためです。
ジグロック18gとジグロック40gを比較すると、多少大きくても重い方が速いですね。
ジグロックの形状なら、表面積の増加による抵抗より、質量の増加の方が速度に与える影響力は大きいと考えられます。
先ほどのシミュレーション①では、ジグロック18gは1.017m/s、ジグロック40gは1.362m/s、メタルジグ18gは1.102m/sだったので、速度順に並べると、
ジグロック40g>メタルジグ18g>ジグロック18g でしたが、
今回のシミュレーション②では順位が変動し、
メタルジグ18g>ジグロック40g>ジグロック18g となりました。
これは面白いですね。
ジグがナナメの状況では、メタルジグ18gのフォールスピードがジグロック40gよりも速くなっています。
これは、メタルジグ18gよりもジグロック40gの2つしか手元にないとき、より長い時間フォールさせて狙いたいときはジグロック40gを選択した方が良いという示唆を与えます。
ウエイトと形状の関係、面白いですね。
シミュレーション④
シミュレーション③の前に、こちらの結果を紹介します。
シチュエーションとしては、水深が10mある深めの防波堤で、足元に落とした状況です。
ロッドティップから海面までにあるラインは風などの抵抗を受けないこととし、海面から水深10mのボトム付近にあるジグは、丁度真下から(ほんのちょい投げなどで)1mブレていると仮定しました。
ジグをぶら下げて静止させた状態から落下させ、水中のジグの姿勢は鉛直下向きになっているとします(入水はまっすぐ鉛直方向。また、既に説明した通り、たとえ姿勢がナナメになった場合でも力のモーメントにより鉛直姿勢になるため)。
④のケースでジグの速度を計算すると、
ジグロック18gは1.655m、ジグロック40gは1.927m、メタルジグ18gは2.127m。
フォール速度はメタルジグの方がジグロックよりも速く、ウエイトがある方が速いという肌感覚と一致しませんか。
それにしても、結構速いですよね。
でも、水深8mくらいのところで水中カメラで観察してみると、確かにこれくらいの速度になっています。
そして、ド真下から1mそれたとはいえ、ほぼ真下に落ちているのでラインはほとんど水を横切らないため、ラインによるジグへの影響はシミュレーション①のように大きくはありません。
ちなみに、ジグロック18gのラインによるジグへの抗力の計算結果は、
シミュレーション①10.23g
シミュレーション②0.056g
シミュレーション③0.065g
となりました。
ラインがジグへ与える力は、ラインの直径だけでなく、ラインがどれだけ水中で動いたかということを考える必要があるということです。
シミュレーション③
これで最後です。
疲れたと思いますが、最後なのでもう少しお付き合いください。
③では、足元でジグの動きを確認するときに行う状況に近いです。
ロッドティップから海面まで5m、水深1m時点のジグのフォール速度です。
④と同様に、ド真下から50cmそれてしまったところにジグがあるものとします。
計算のポイントは④とほぼ同じなので省略します。
こちらも、ジグをぶら下げて静止させた状態から落下させ、ジグの姿勢は鉛直下向きになっているものとします。
さて、気になる計算結果は、
ジグロック18gは1.659m、ジグロック40gは1.929m、メタルジグ18gは2.133m。
1秒間で1.6m~2.2mくらいの落下距離です。
④と比較すると順位は変わりませんが、ラインのブレが50cm分少ないので、水の抵抗が減り、若干速度が増したと考えられます。
みなさんも足元でジグを動してみると、このくらいの速度でフォールすることを確認できるのではないでしょうか(実際には、フラッシングを確認するために入水角度を斜めにしていると思いますが…)。
シチュエーション③と④を見てみると、ラインにかかる水の抵抗がなければ、ジグは結構速い速度で落ちていくことがわかります。
それだけ、ラインにかかる水の抵抗はジグの速度に与える影響が大きいということになります。
リフトアンドフォールのアクションをするときにフォール時間を長くとり過ぎると、釣果が落ちたり、根掛かりしてしまいます。
ジグの形状、飛距離、ウエイトによって、フォール時間を変えなくてはいけないということが理論的にもわかりましたね。
実釣では、風によるラインへの抵抗、潮によるラインとジグへの抵抗、フックの抵抗、使用するタックルなども考慮しなくてはいけません。
だから、同じようにアクションしていても日によって釣果に差が出るということや、同じジグを使っていても隣の人と釣果に差が出るということが起こりうるわけです。
しかし、結局いろんな要素があるから「考えてもわからない」ではなく、今の状況ではこの要素が強いのでないかと仮説を立てて検証みると、釣りが上手になるはずです。
100均ジグの釣りが上手くなるちょっとしたコツについては、他の記事や動画で紹介していますので、もし良かったら見てみてください。
アクションについては、ただ巻きとリフト&フォールをマスターすれば応用出来るようになるので、動画で紹介しています。
まとめ
まず、お疲れ様でした。
大変読みづらい内容だったと思いますが、ここまで読んでいただきありがとうございました。
今回の記事は、細かい計算結果よりもどういう要素がフォール速度とフォール姿勢に影響を与えるのか、何かしらヒントになることはあったのではないかと思います。
数字アレルギーの方にはこの感覚はわからないと思いますが、数学に慣れている人には「速度の2乗が抗力に影響を与えるのね、なるほど」といった発見があったと思います。
再度私が重要だと思う点をおさらいします。
・ショアジギングでは、ラインに対する水の抵抗がジグのアクションに与える影響が大きい
・水平姿勢になったジグには、ラインにかかる水の抵抗でいずれ鉛直上向き姿勢(気をつけ!)になる
・100均ジグのフォール姿勢は、ほとんどの状況で鉛直上向き姿勢になっていると考えて良い
・同じウエイトなら、ほとんどの状況でフォールはメタルジグの方がジグロックよりも速い
・浮力はフォールアクションにほとんど影響しない
・目に見えているジグの動きは、ほんの一部に過ぎない
今回紹介したシミュレーションは4パターンでしたが、実は他にも数パターン行っています。
一般的なシチュエーションではないのと、もうこれ以上はたくさん!という声が聞こえてきそうなので、紹介はしません。
また、手計算というのは大げさではなく、紙とペンと計算機を使って実際に計算しました。
もちろん、一旦式が出来上がったあとは、計算ソフトを使用しています。
だいぶ経験則と合致する結果にはなりましたが、物理のセンスはまるでありませんので、根本の式(力の釣り合いの式)の立て方を間違っていたり、単位が間違っている可能性もありますのであくまで参考程度にお考え下さい。
さて。
これは100均ジグのフォール時についての話でした。
冒頭にも記載しましたが、2022年は100均ジグのパートナーを探すため、メーカージグをいくつか買って試釣をしています。
メーカージグを購入した時点では今回のような計算はしていなかったので、感覚的にフロントウエイトや左右非対称が良いのではないかと模索していました(気になる方はその際の記事をご参照ください)。
今回計算式を作ったことで、数値を変えれば他のジグの速度も計算できますし、どの要素がどのようなアクションに影響を与えるかが少しずつわかってきました。
ジグの形状を見て、このジグはこのアクションが良さそうだなというのが、よりはっきり見えてきました。
この記事の執筆時点ではメーカージグを5つ購入して試釣しましたが、こうなってくると他にもいろいろと試してみたくなってきました。
世の中には、誰が使っても釣果が出やすいジグは確かにあると思います。
しかし、使い手によって結果ががらりと変わるジグがあることも、おそらく間違いないです。
おそらく、製作者すら思いついていない使い方もあると思います。
どんなジグを使ったとしても、そのジグが持っている力を引き出せるように今後も研究していきたいですね。
それに、今回の出来上がった計算式を眺めていると、リアバランスでリアフックに絡んでしまう場合はあのアクションをやっているかもしれない とか、ジグアクションのピッチが一定になる条件はこれっぽいな とかいろいろ浮かんできてわくわくします。
あ、このサイトは100均ジグを使用してのショアジギングがテーマでしたね。
つい他のジグに浮気してしまいそうになりました。
でも、100均ジグの釣りを研究すると他のジグでの釣りにも活かせますし、逆もまた然りですね。
100均ジグ、バンザイ!!

 https://fp-org.com/partner/
https://fp-org.com/partner/







ディスカッション
コメント一覧
まだ、コメントがありません