リトリーブ中のジグの角度の計算方法
突然ですが、普段使っているジグの絵を、3秒以内に空に描いてみてください。
(よろしければ、やってみてください。)
描けましたでしょうか。
ジグを真横に描いた方は、この記事で新たな発見があるかもしれません。
では、本題に入ります。
「リトリーブ中のジグの角度」について、考えたことはありますでしょうか。
一定以上のスピードでジグをタダ巻きしているときは、多くのケースで、ジグの角度はラインを引っ張る角度とイコールになります。
ラインを引っ張る角度は、遠投すると水面に対して平行に近くなり、ピックアップ(回収)直前は水面に対して直角に近くなります。
ここまでは、簡単に理解できます。
では、具体的に何度くらいの角度なのかというと、
ほとんどの人が学校で習ったはずの知識と検索サイトを使えば、計算することができます。
次の画像をご覧ください。
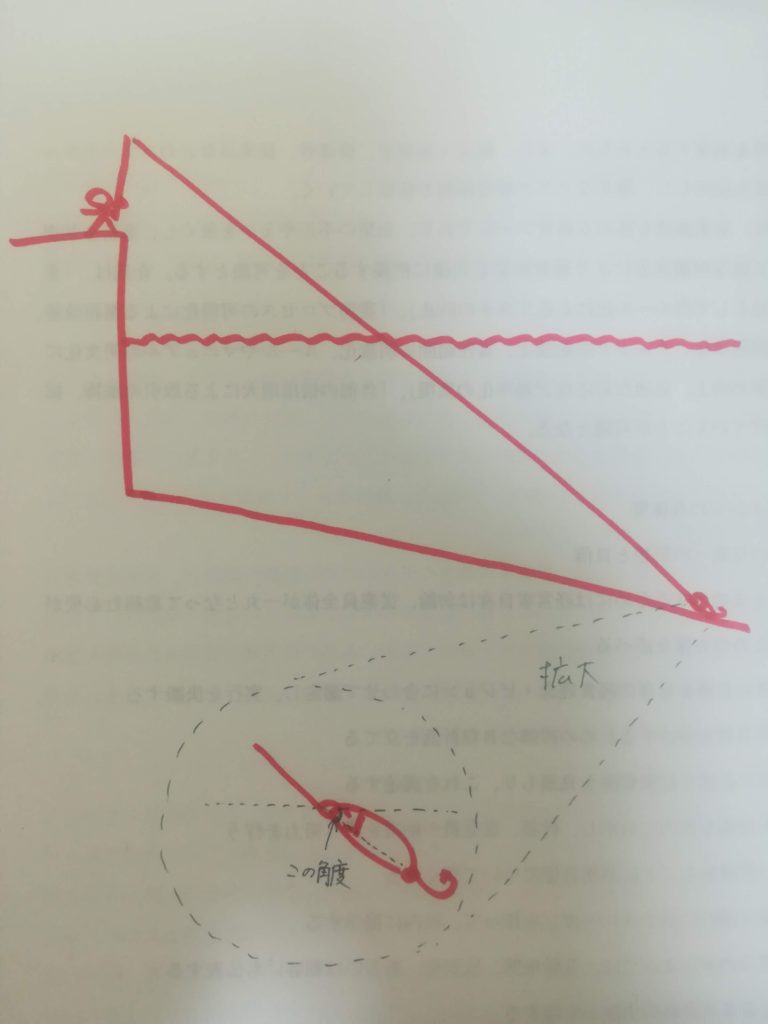
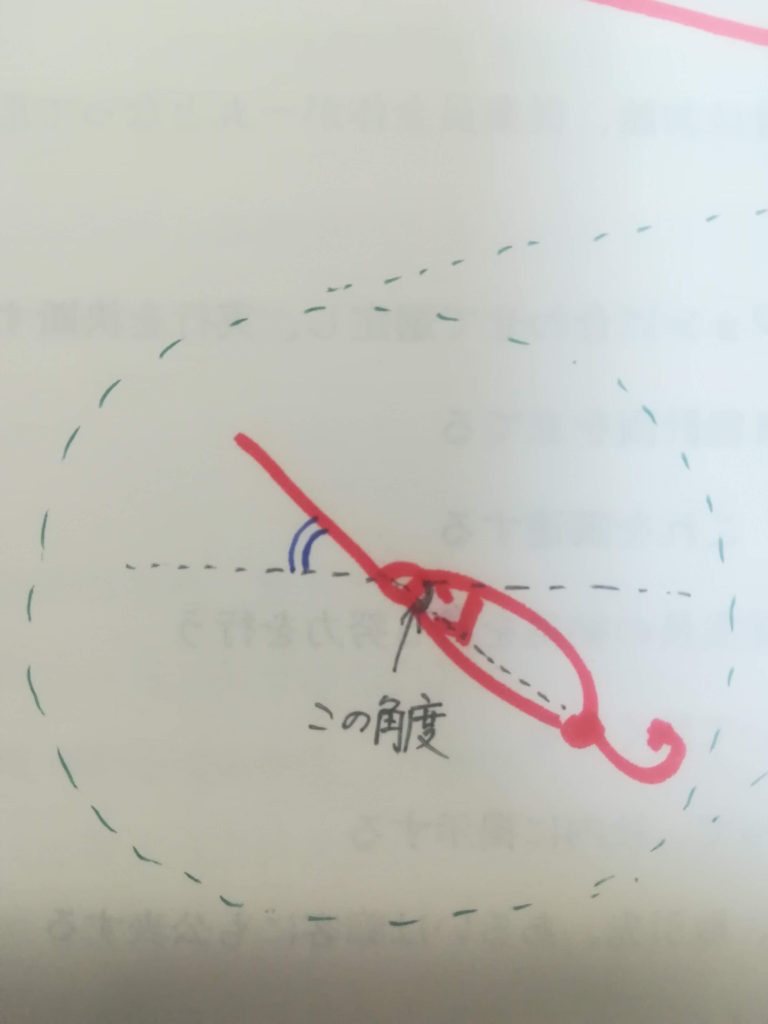
上の図は、ルアーがボトムに着いて、ラインを張ったときをイメージしています。
この時のルアーの角度について計算してみます。
下の図をご覧ください。
ルアーの角度は、黄色い直角三角形を考えたときの、「海面と平行な海底とルアーの角度」と同じになります。
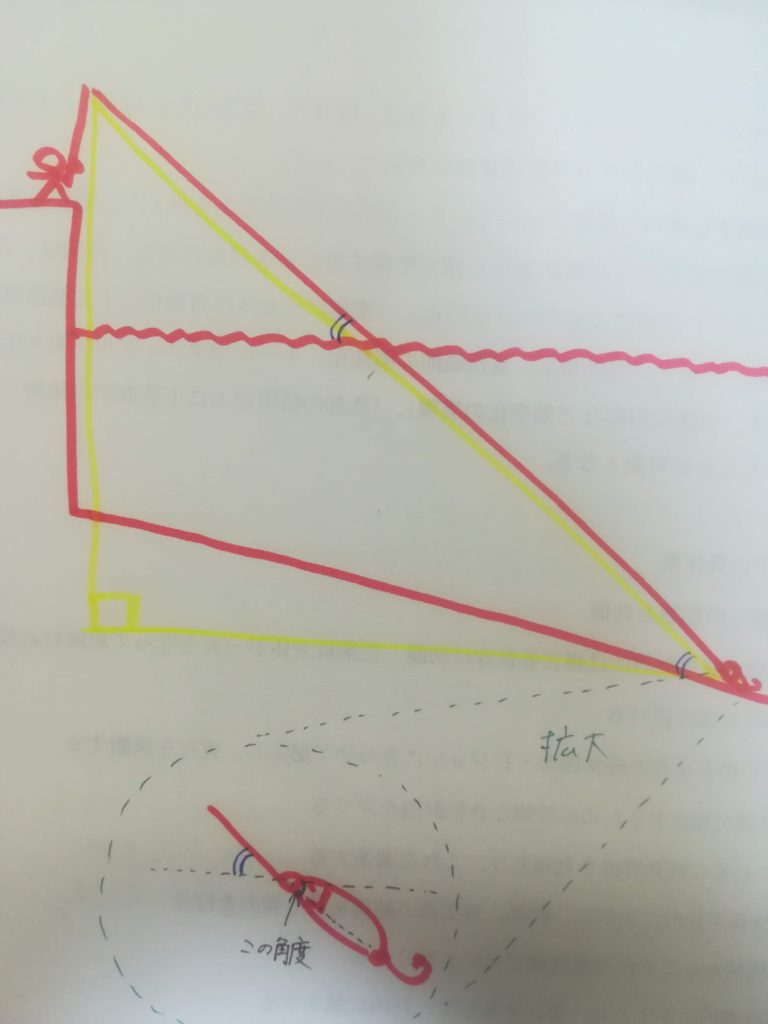
ここで、具体的な数字を書き込んでみます。
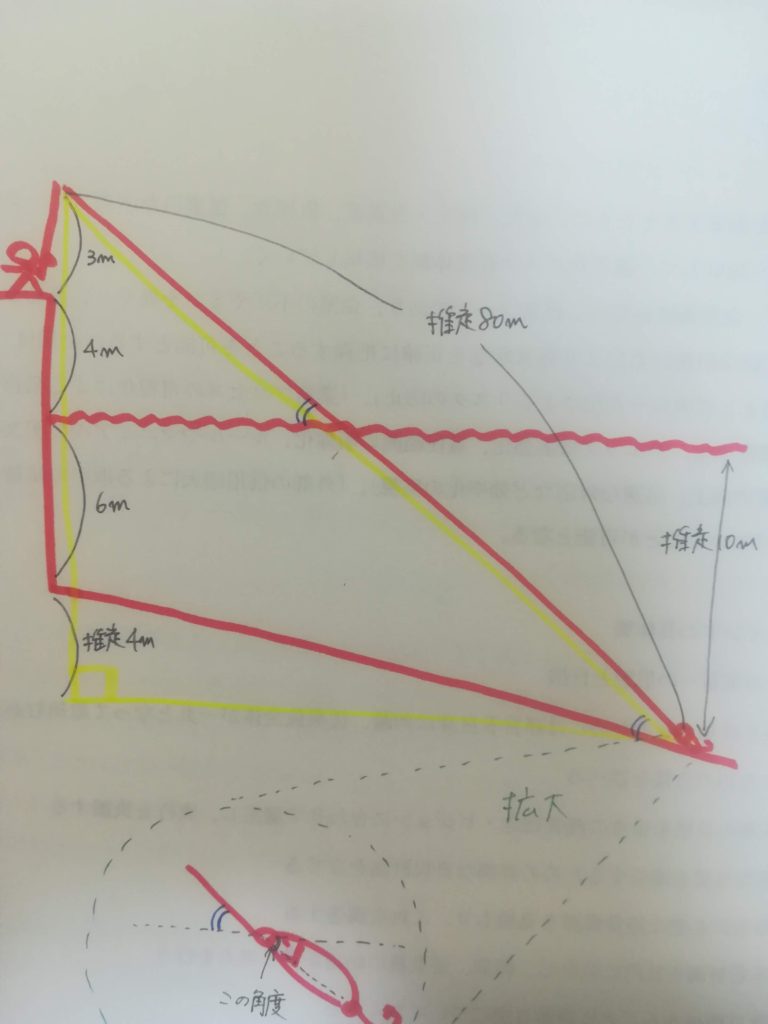
次の図をご覧ください。
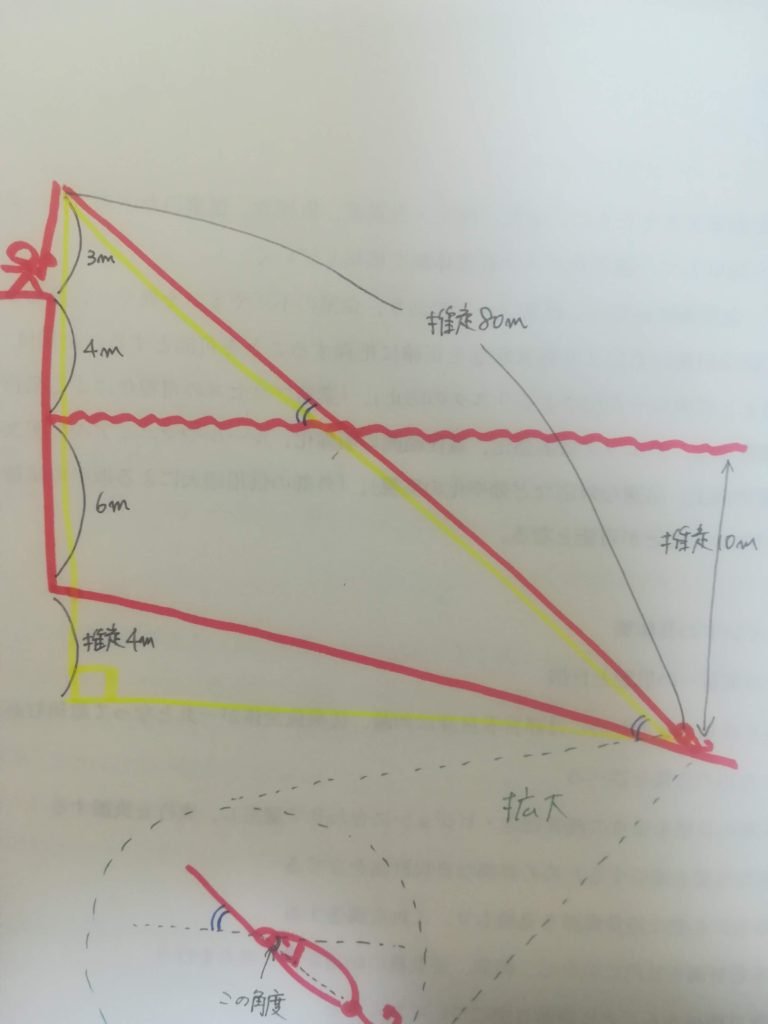
ラインが推定80メートル出ていて、竿先から水面まで7メートル、水深10メートルとすると、
黄色い三角形について考えてみると、
一番長い辺(斜辺)は80メートル、1辺(高さ)が17メートルの直角三角形となります。
ここで、学校で習った知識を利用します。
サイン・コサイン・タンジェント です。
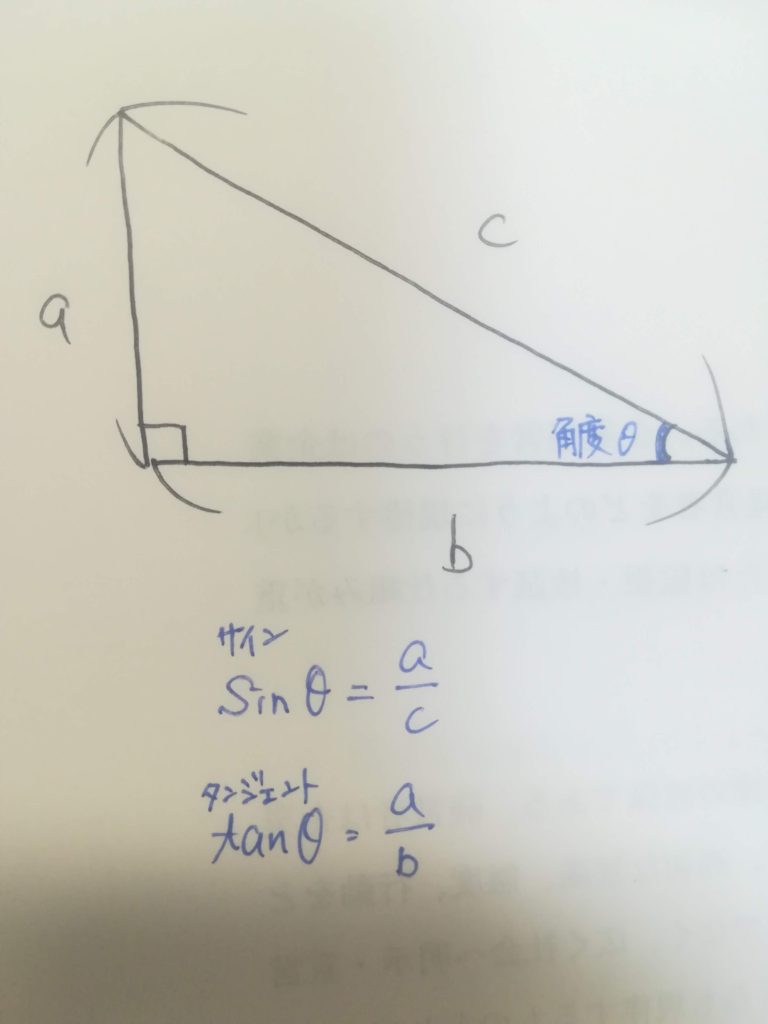
図を見比べてみてください。
a=17メートル、c=80メートル、ルアーの角度=θ(シータ)となっていることがわかりますでしょうか。
sinθ=a/c(←これは公式)なので、sinθ=17/80を解けば、ルアーの角度が出てくると言うわけです。
実際に、計算サイトを使って入力してみると、
(計算サイト https://www.calc-site.com/triangles/trigonometric_angle/1
※図のaは、計算サイト上ではbに置き換えてください。)
θ≒12.268と出てきました。
つまり、ルアーの角度は約12度ということになります。
別の例として、ラインが50メートル出て、水深が推定9メートルの場合、
sinθ=16/50を解くと、θ≒18.66と出てきましたので、約18.6度ということになります。
では最後に、ルアーを足元まで泳がせてきて、ピックアップするときを想定すると、
ラインは14メートル出ていて、水深が6.5メートルとすると、
sinθ=13.5/14を解くと、θ≒74.64と出てきましたので、約75度ということになります。
ルアーを回収し、釣り人に近くなってくればくるほど垂直に近くなるのは、経験していますよね。
ちなみに、tanθというのもありまして、
人から着水するまでの水平方向の飛距離をbとすれば、tanθ=a/bを解けば同様にルアーの角度θが求められます。
蛇足ですが、cosθ=b/cを解いても同じ角度が出ます。
直角三角形を考えたとき、どこか2辺がわかれば、サイン、コサイン、タンジェントのどれかが使えるので、ルアーの角度が導き出せるというわけです。
cやbについては、10メートルごとに色の変わるラインなどを巻いていればだいたいわかりますし、
ハンドル1回転で何センチ巻けるか予め調べておき、釣り場でボトムにジグが着いてから回収できるまでのハンドルの回転数から計算しても、ざっくりとした数字はわかります。
a(水深)については、通常は推定するしかありません。
思い出しながらの記事になりましたので、誤りがあるかもしれません。
ご指摘いただければ、修正します。
なお、ラインスラックを考慮に入れていないことなど、上記は厳密な測定方法でないことはご理解くださいね。
さて、いかがだったでしょうか。
遠投すればするほど、水深が浅ければ浅いほど、ジグは水平に近くなります。
水深が深ければ深いほど、ジグは垂直になります。
ジグの角度は、ライン放出量と高さ(竿先から水面までの高さ+水深)によって異なるということですね。
さて、ここで、疑問が湧いた方はいませんでしょうか。
遠浅のサーフで遠投し、リフト&フォールをしようとしたとき、
ラインの角度はほとんど水平に近くなります。
ということは、「リフト」は本当に出来ているのでしょうか。
次回、ルアーの角度について、もう少し掘り下げて考えてみる予定です。








ディスカッション
コメント一覧
まだ、コメントがありません